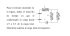Page 1 jlr marrero 2 II. AN ´ALISIS DE CIRCUITOS EN R´EGIMEN

Page 1 jlr marrero 2 II. AN ´ALISIS DE CIRCUITOS EN R´EGIMEN

jlr marrero
2
II. A N ÁLISIS DE CIRCUITOS EN R ÉGIMEN SENOIDAL PERMANENTE
En estas notas analizamos la respuesta en frecuencia de circuitos lineales con elementos almacenadores de energı́a
(capacidades y/o inductancias). Es decir, estudiamos la respuesta forzada del circuito cuando la excitación es senoidal,
cos ωt. Estos circuitos se caracterizan por ser selectivos en frecuencia.
Como
ejωt = cos ωt + j sin ωt
⇒
cos ωt = Re{ejωt }
y el circuito es lineal, estudiaremos la respuesta del circuito a una excitación del tipo ejωt , denominada exponencial
compleja. Una propiedad de los sistemas lineales es que si la excitación es del tipo ejωt , también lo es la respuesta,
ası́ como todas las variables del circuito. Es decir, si la excitación es x(t) = ejωt , la respuesta será y(t) = H(jω) ejωt .
Como el circuito es lineal, la respuesta del circuito cuando la entrada es x(t) = cos ωt será
y(t) = Re{H(jω) ejωt }
Si expresamos H(jω) = |H(jω)| ejφ , la respuesta se puede escribir
x(t) = cos ωt
⇒
y(t) = |H(jω)| cos(ωt + φ)
(1)
Las funciones |H(jω)| y φ(ω) nos dan información sobre la respuesta de un circuito cuando la excitación es senoidal. A
esta información se le conoce como respuesta en frecuencia del circuito.
i
+
−
v
C
Antes de analizar un circuito complejo, consideremos primero la relación entre la tensión y la corriente en un condensador (ver figura). Si aplicamos una tensión exponencial compleja al condensador, la corriente viene dada por:
v(t) = V ejωt
⇒
i(t) = C
dv
= jωC V ejωt ≡ I ejωt
dt
⇒
I = jωC V ≡ V /ZC
donde ZC = 1/(jωC) es la impedancia del condensador. De forma análoga, la impedancia de una bobina es ZL = jωL,
mientras que para una resistencia es ZR = R. Es decir, la relación entre las amplitudes complejas V e I es similar a la
ley de Ohm, V = Z I.
Estudiemos ahora el circuito RC de la figura usando esta idea. Usando las reglas de Kirchoff podemos escribir
v(t) = vC (t) + vo (t)
⇒
V ejωt = VC ejωt + Vo ejωt
⇒
V = VC + Vo
⇒
V = ZC I + ZR I
donde hemos usado el hecho de que la corriente es la misma en todos los elementos. Por tanto, la relación entre las
amplitudes complejas de vo (t) y v(t) es
Vo = I ZR
⇒
i
Vo =
ZR
V ≡ H(jω) V
ZR + ZC
(2)
C
vo
v
+
−
+ vC −
R
Es decir, el circuito RC es un divisor de tensión, muy parecidos a los divisores de tensión resistivos. Éstos tratan por
igual a las señales variables en el tiempo y a las señales DC. En cambio, si el divisor de tensión tiene capacidades, la
respuesta del divisor depende la frecuencia de la señal, ya que la impedancia del condensador depende de la frecuencia.
Esto es debido a que los condensadores tienen “inercia”: la tensión en bornes de un condensador no cambia bruscamente.
jlr marrero
3
Si la excitación en el circuito RC es v(t) = V cos ωt, entonces (1) nos indica que la respuesta es
vo (t) = |Vo | cos(ωt + φ) = V |H(jω)| cos(ωt + φ)
donde H(jω) viene dado por (2). La amplitud de la tensión senoidal de salida es proporcional a la amplitud de la tensión
senoidal de entrada, donde la constante de proporcionalidad es función de la frecuencia:
jωRC |Vo | = V |H(jω)| = V 1 + jωRC donde hemos usado las impedancias de la resistencia y el condensador, ZR y ZC respectivamente. Si definimos la frecuencia de corte ωo ≡ 1/RC, la amplitud de la tensión de salida se puede escribir como
jω/ωo |Vo | = V 1 + jω/ωo Si ω ≫ ωo
|Vo | ≈ V
φ≈0
Es decir, el circuito deja pasar la señal sin atenuación y en fase con la entrada. En cambio, si ω ≪ ωo
ω
π
|Vo | ≈ |jω/ωo | V =
V
φ≈+
ωo
2
Cuanto menor sea la frecuencia respecto a ωo , menor es la amplitud de la señal senoidal de salida. La componente continua
de la señal no pasa porque su frecuencia es nula. Un circuito con esta respuesta en frecuencia se denomina filtro paso-alto.
La figura muestra los diagramas de módulo y fase de la respuesta en frecuencia en escala logarı́tmica. Estos gráficos
tienen la ventaja de representar grandes dominios de las variables, suavizando las variaciones de la función. Observe que
casi todo el cambio de fase tiene lugar en dos décadas de frecuencia, alrededor de la frecuencia de corte del filtro. En esta
gráfica se observa muy bien que la ganancia se degrada por debajo de la frecuencia de corte, reduciéndose en un factor de
diez por cada disminución de una década en frecuencia.
1
0.1
módulo, |H(jω)|
0.01
ω/ωo
0.01
0.1
1
10
+π/2
fase, φ
≈ 6o
+π/4
0
≈ 6o