8. Describa geométricamente el conjunto de todos los complejos del
Transcripción
8. Describa geométricamente el conjunto de todos los complejos del
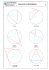
8. Describa geométricamente el conjunto de todos los complejos del plano (puntos), que satisfacen las relaciones siguientes. a) e) z−i = 1 z −1 + z +1 = 6 c) Re z = 3 b) 1 ≤ z − i f) d) Re z > 3 z + z = Im z . Solución: 2i a) El lugar geométrico está formado por los complejos z que están a distancia 1 de i. ste es la circunferencia con centro i y radio 1 i b) Aquí el lugar geométrico es el conjunto de los complejos z que están en la circunferencia anterior ( z − i = 1 ) y los que están fuera de ella c) ( z − i > 1 ). Re z = x = 3 define la recta paralela al eje imaginario y a distancia 3 de él 3 d) Re z = x > 3 define el semiplano a la derecha de la recta anterior; la recta no es parte del lugar geométrico 3 3i e) tenemos que z pertenece al lugar geométrico si la suma de sus distancias a los complejos 1 y -1 es igual a 6. Esto es una elipse, con focos a = 3, c= 2, y b= 5 F1 = (-1 , 0) F1 F2 -1 1 F2 , f) esto equivale a 2x = y, cuya representación geométrica es la recta de la figura. 3 = (1, 0) 2i 1 9. Sea p ( z ) = a 0 z n + a1 z n − 1 + ....... + a n un polinomio con coeficientes reales. Demostrar que si w ∈ C es un cero de p(z) , entonces w es un cero de p(z). Dar un ejemplo para mostrar que esto no es válido si los coeficientes son complejos. Solución: * p ( w) = 0 ⇒ p ( w) = 0 = a 0 w n + a1 w n −1 + .... + a n = a 0 w n + a1 w n − 1 + .. .. + a n = a 0 w n + a1 w n −1 + .... + a n = a 0 w n + a1 w n − 1 + . . . . + a n = p (w) , pues a 0 , a1 , . . . . , a ∈ R k y una aplicación del Teor. 2 (5), prueba que w k = w . (Teor. 2, (4)) (Teor. 2, (5)) Como p ( w) = 0 , w también es un cero de p. ** w = 1 − i es un cero de p ( z ) = iz − i −1, pero w = 1 + i no lo es. 10. Suponga que a ∈ C , a < 1. Demuestre que ⎧ < 1 , si z < 1 ⎪ ⎨ = 1 , si z = 1 ⎪ ⎩ > 1 , si z > 1 z − a 1 − az Solución: z−a 2 − 1− az 2 = z = z = z 2 + a 2 2 + a 2 + a 2 = ( z = ( z 2 − z a − za − (1 + a z 2 2 −1− a z −a − 1− az ( 1− az )2 z ( z 2 2 − 1) 2 2 > 0 , de modo que ⎧ < 0 , si z < 1 ⎪ ⎨ = 0 , si z = 1 ⎪ ⎩ > 0 , si z > 1 2 Dividiendo miembro a miembro por z −a 2 2 − 1) (1 − a ) Siendo a < 1 , tenemos que 1 − a 2 − az − a z) − 1 − a z , (a z = a z ) − 1) − a 2 2 2 1 − a z , en cada caso obtenemos ⎧ < 0 , si z < 1 ⎪ − 1 ⎨ = 0 , si z = 1 ⎪ ⎩ > 0 , si z > 1 De aquí se sigue la relación por demostrar: Nota: 1 − az 2 = 0 si ⇒ z = a −1 = a z = a −1 −1 > 1; luego, en el último caso hay que excluir esta posibilidad. 11. Demostrar que la ecuación de cualquier circunferencia puede escribirse en la forma 2 y b ∈ C. a z + bz + b z + c = 0 , donde a , c ∈ R Solución: r Según sabemos, la ecuación de la circunferencia con centro en w y radio r > 0 , es de la forma z w Ax 2 + Ay 2 + Bx + Cy + D = 0 siendo z = x + yi. Esta se puede escribir como sigue: A ( x 2 + y 2 ) + B Re z + C Im z + D = 0 A z A z A z 2 1 1 + B ( z + z ) + C (z − z ) + D = 0 2 2i 2 + ( B C B C − ) z + ( + )z + D = 0 2 2i 2 2i 2 +( B C B C + i) z + ( − i)z + D = 0 2 2 2 2 b: = Poniendo a : = A , B C + i, 2 2 (Teor. 2 , (3) ) c : = D, la ecuación de la circunferencia queda escrita: 2 a z + bz + b z + c = 0 con a ., c ∈ R b ∈ C. y 12. Demostrar que ∀ z ∈ C : x + y 2 ≤ z ≤ siendo z = x + yi Solución: z = x2 + y2 ≤ x 2 + y 2 + 2 xy (pues 2 xy ∴z ≤ ( x + y )2 = x Por otra parte, de ( x + ≥ 0) + y . y )2 ≥ 0 obtenemos x + y , 2x y ≤ x2 + y2 . Sumando x 2 + y 2 a cada miembro 2 x y + x2 + y2 ≤ 2 ( x2 + y2 ); esto es ( x + luego: y )2 ≤ 2 z x + y ≤ 2 ; 2 z