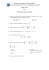1. Considere la forma canónica general de un sistema de dos

1. Considere la forma canónica general de un sistema de dos

1. Considere la forma canónica general de un sistema de dos ecuaciones lineales con dos
incógnitas:
a11 x + a12 y = b1 ,
a21 x + a22 y = b2 ,
donde aij ∈ R, i, j = 1, 2.
(a) Deduzca cuáles son las condiciones para que el sistema sea consistente/inconsistente.
Argumente1 su respuesta.
(b) Establezca la interpretación geométrica de las condiciones anteriores.
2. Mediante eliminación de Gauss-Jordan lleve las siguientes matrices2 a su forma
escalonada reducida (si existe).
(a)
−1 −1
2 5
2
3 −1 1
(b)






−1
−2
3
−4
5

8
2
7 −1 

6
3 

1
8 
0
0
3. Considere el siguiente sistema de ecuaciones lineales:
x + py = 6,
−2x + 3y = q
donde x, y son la variables y p, q son constantes reales pero cuyo valor aun no se ha
determinado. Encuentre para que valores de p y q el sistema anterior:
(a) no tiene solución,
(b) tiene una solución única,
(c) tiene infinidad de soluciones.
1
2
Justifique con un desarrollo lógico.
Aquı́ la matriz NO tienen la interpretación de un sistema de ecuaciones.
1
4. Considere el siguiente sistema de ecuaciones lineales:
x+y+z = 1
−x − 2py = −1,
2x − 3y = q
Encuentre para que valores de p y q el sistema anterior:
(a) no tiene solución,
(b) tiene una solución única,
(c) tiene infinidad de soluciones.
5. Determine todas las matrices 2×2 reales de la forma A =
a 0
b c
tales que A2 = 1.
6. Sean A y B matrices cuadradas, demuestre lo siguiente
(AB)T = B T AT
7. Pruebe que si las matrices A y B tienen inversa, entonces
(AB)−1 = B −1 A−1
8. Considere a la matriz


−1
2
2
A =  0 −2 −1 
1 −3 −1
Encuentre el determinante de A y calcule a su matriz adjunta, adj(A).
9. Utilizando las propiedades del determinate (sin desarrollarlo) verifique si la siguiente
afirmación es falsa o verdadera:
1 1 1 1 a a2 a b c = 1 b b2 .
bc ac ab 1 c c2 10. Encuentre la inversa de las matrices A, B y

−1
−1 2
A=
,
B= 2
2 4
0
C

0
2
1 −1  ,
2
1
A=
1 2
2 1
11. Pruebe que el determinante de una matriz A y su transpuesta, son iguales. Es decir
det(A) = det(AT )
2
12. Determine si los vectores v1 = (1, 0, 1, 2)T , v2 = (0, 1, 1, 2)T y v3 = (1, 1, 1, 3)T son
linealmente independientes, o linealmente dependientes.
13. Determine si los vectores v1 = (1, 2, −1)T , v2 = (1, −2, 1)T , v3 = (−3, 2, −1) y v4 =
(2, 0, 0)T son linealmente independientes, o linealmente dependientes.
14. Pruebe que si V = R3 , que los vectores v1 = (1, 1, 0)T , v1 = (1, 0, 1)T y v3 = (0, 0, 1)
son una base de V.
3