Rectas Secante y Tangente - Introducción

Rectas Secante y Tangente - Introducción

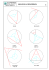
Rectas Secante y Tangente - Introducción
Nota:
f(x) es una función cualquiera
a, Xa y Xb son valores cualesquiera de x
Δx es una distancia cualquiera
entre dos valores del eje x
Introducción
Comenzaremos a analizar el crecimiento y decrecimiento de las funciones que
estudiemos, a tal efecto, necesitamos una nueva herramienta que nos permita sacar
conclusiones sobre dichas características. La herramienta que propondremos será simple y
sencilla: a través de la función que queramos estudiar trazaremos ciertas rectas y
estudiaremos sus características para deducir cómo se comporta la función original.
Definiciones
Una recta secante es aquella recta que corta a una curva en dos puntos (al menos), a
medida que estos dos puntos elegidos se van acercando la recta secante tiende a
convertirse en una recta tangente.
Una recta tangente es aquella recta que se “apoya” en un punto de una curva,
manifestando cual es la dirección que toma la curva para ese punto.
En el siguiente gráfico pueden observarse una curva (azul), tres secantes (roja, amarilla y
verde) y una tangente (magenta)
(Gráfico 1)
1
Recta Secante y Tangente – Matemática – Escuela Técnica ORT – 2013 – Ezequiel Wajs
Cálculo de la Recta Secante
En principio nos interesaremos sólo por averiguar la pendiente de las rectas Secante y
Tangente y comenzaremos con el cálculo de la pendiente de la recta secante.
Es importante notar que para calcular la pendiente de la recta secante no es necesario
conocer el gráfico de la función ni ninguna propiedad de la misma más allá de su dominio
y su expresión matemática.
Si la recta secante corta a la curva (la función) en dos puntos, quiere decir, precisamente,
que aquellos dos puntos en donde la recta corta a la curva son comunes a ambas, es
decir, son parte de la recta secante y parte de la curva a la vez. Por lo tanto, en esos dos
puntos, la recta y la curva “comparten” sus coordenadas (x;y). Estos dos puntos son
escogidos arbitrariamente, sin ningún criterio en especial.
Llamemos a las abscisas de esos dos puntos (coordenadas del eje x) Xa y Xb, e
imaginemos un gráfico ficticio de una función cualquiera:
f(Xb)
f(Xa)
Δx
Xa
Xb
(Gráfico 2)
Es evidente que, como muestra la figura, sean cuales fueren Xa y Xb, sus respectivas
imágenes (ordenadas) serán f(Xa) y f(Xb), (es decir, la función reemplazada en Xa y en Xb
respectivamente).
2
Recta Secante y Tangente – Matemática – Escuela Técnica ORT – 2013 – Ezequiel Wajs
Una vez comprendido que para hallar dos puntos de la recta secante (especificamente los
dos puntos de intersección) no hace falta conocer nada más que la expresión algebráica
de la función (y su dominio) estamos listos para hallar la pendiente de dicha recta.
Recordando que la pendiente de una recta (m) puede calcularse con la expresión:
=
m
∆y y2 − y1
=
∆x x2 − x1
Siempre y cuando (x1;y1) y (x2;y2) sean dos puntos distintos de la recta.
En el caso de la recta secante estos dos puntos necesarios son los únicos dos puntos de la
recta que se conocen (y que pertencen también a la función) son:
( Xa; f ( Xa) )
( Xb; f ( Xb) )
Por lo tanto la expresión de la pendiente de la recta secante es:
m=
sec
∆y
=
∆x
f ( Xb) − f ( Xa )
=
Xb − Xa
f ( Xa ) − f ( Xb)
Xa − Xb
Otra forma de escoger los dos puntos distintos de la recta es fijar uno y definir al otro a
través de la distancia a la que se encuentra del primero. En el caso del Gráfico 2 (pág. 2),
podríamos definir Xa como el punto y Δx como la distancia al segundo punto (por lo
tanto no necesitaríamos saber Xb). De esta forma las coordenadas de los dos puntos
quedan:
( Xa; f ( Xa) )
( Xa + ∆x; f ( Xa + ∆x) )
m=
sec
∆y
=
∆x
f ( Xa + ∆x) − f ( Xa )
=
Xa + ∆x − Xa
f ( Xa + ∆x) − f ( Xa )
∆x
Estas dos formas de hallar m son totalmente análogas, puede usarse cualquiera. Este
segundo método se conoce como cociente incremental.
3
Recta Secante y Tangente – Matemática – Escuela Técnica ORT – 2013 – Ezequiel Wajs
Ejemplo:
Se tiene la función
f ( x=
) x2 + 2x
cuyo gráfico se desconoce por completo. Calcular la
pendiente de la recta secante a la función en los puntos X=0 y X=2.
=
Xa 0=
Xb 2
f ( Xa ) = f (0) = 02 + 20 = 1
m=
sec
∆y
=
∆x
f ( Xb) = f (2) = 22 + 22 = 8
f ( Xb) − f ( Xa ) f (2) − f (0) 8 − 1
=
=
= 3,5
Xb − Xa
2−0
2
Analizando el signo y el valor de la pendiente de la recta secante pueden obtenerse varias
conclusiones acerca de lo que sucede con la función f(x) dentro del interválo (0;2).
El signo de la pendiente de una recta indica la dirección que tiene esa recta, si el signo es
positivo, la recta es creciente, si es negativo, es decreciente (al mismo tiempo si la
pendiente es 0 la recta es una constante).
Sería cierto en varios casos (pero no en todos) decir que si la pendiente de la recta
secante es positiva la función crece y si es negativa, decrece. Sin embargo podría darse el
caso de que se elijan dos puntos entre los cuales la función pase de crecer a decrecer en
una o más ocasiones, por ejemplo:
(Gráfico 3)
4
Recta Secante y Tangente – Matemática – Escuela Técnica ORT – 2013 – Ezequiel Wajs
Puede verse en el Gráfico 2 (pág. 2) que la pendiente de la recta secante es positiva y que
la función crece, sin embargo, en el gráfico 3 aquí presentado la pendiente de la recta
secante es positiva y la función no es estrictamente creciente, sino que de a momentos
crece y de a momentos decrece. Si es cierto, sin embargo, que crece más de lo que
decrece para los dos puntos escogidos. Por lo tanto, a efectos de estudiar el crecimiento
de la función, la recta secante es una forma aproximada, no exacta.
Cálculo de la Recta Tangente
Para evitar la aproximación que se produce al calcular la pendiente de la recta secante la
primer solución que podemos proponer es no tomar dos puntos muy distantes, sino dos
puntos muy cercanos, de esa forma, estaríamos analizando un tramo más pequeño y la
probabilidad de que la función varíe mucho en ese tramo disminuye, sin embargo,
mientras el tramo sea finito, estaremos aproximando. Poder analizar el crecimiento y
decrecimiento punto a punto sería ideal, dado que no habría aproximación alguna, al
mismo tiempo, nos encontramos con el problema de que no puede definirse una sola
recta con un único punto. Sin embargo, si existe una recta única que “depende” de un
único punto de la función, llamada recta tangente y que en ese punto en donde se
“apoya” sobre la función, llamado punto de tangencia, tiene la misma dirección y sentido
que la función:
(Gráfico 4)
5
Recta Secante y Tangente – Matemática – Escuela Técnica ORT – 2013 – Ezequiel Wajs
Fue a mediados del 1600 que dos matemáticos, Newton y Leibniz, independientemente,
encontraron una solución. La solución fue no dejar de tomar dos puntos para hallar la
secante, pero si imponer la condición de que esos dos puntos fueran infinitamente
próximos (es decir, que los puntos elegidos tienden a ser los mismos), de modo que esa
recta secante tienda a convertirse en una recta tangente y de esta forma calcular de
manera exacta y sin aproximar, una pendiente (de la recta tangente) que permita analizar
de forma precisa el crecimiento y decrecimiento de las funciones. Si en vez de llamar Xa y
Xb a los puntos, llamamos “a” al punto en donde queremos hallar la pendiente de la recta
tangente y “x” al punto que tiende a ser a. De esta forma e imaginando a la tangente
como al límite de una secante podríamos utilizar el mismo método que el usado antes en
estas páginas para hallar su pendiente, llamaremos a ese valor derivada de la función en
el punto “a” y se escribirá f’(a):
Los dos puntos ahora son
( x; f ( x) ) y ( a; f (a) )
Y la pendiente de la recta tangente evaluada como el límite de la secante cuando a y x son
infinitamente parecidas:
f ′(=
a ) m=
tg
∆y
f ( x) − f (a)
= lim
∆x x →a
x−a
Y cuando utilizamos la forma de cociente incremental (si solo definimos un punto “x” y la
distancia al otro punto “Δx”), lo que sucede ahora es que en vez de hacer que un punto
tienda a ser el otro, proponemos que la distancia entre ambos puntos tienda a ser cero.
f ′(=
a ) m=
tg
∆y
f (a + ∆x) − f (a )
= lim
∆x ∆x →0
∆x
Nuevamente, estas dos formas de calcular la pendiente son totalmente análogas y arrojan
exactamente los mismos resultados, aunque la operatoria para llegar a ellos pueda ser
levemente distinta.
6
Recta Secante y Tangente – Matemática – Escuela Técnica ORT – 2013 – Ezequiel Wajs
Ejemplo:
Se tiene la función
f ( x) = x 2 + 2 x + 1 cuyo gráfico se desconoce por completo.
Calcular la pendiente de la recta tangente a la función en el punto X=3. Coloreamos los
términos que son los mismos, paso a paso.
Método 1
Puede verse que el punto elegido es a = 3 y f(3) = 16.
De esta forma el límite queda:
f ′(3)
= m=
tg
∆y
f ( x) − f (3)
= lim
∆x x →3
x −3
Como x es una variable que tiende a “a” y lo mismo para f(x) no pueden ser
reemplazadas por a hasta no resolver la indeterminación, solo podemos
reemplazar f(x) por su expresión algrebráica:
x 2 + 2 x + 1 − 16
x 2 + 2 x − 15
f ′(3) lim
=
= lim
x →3
x →3
x −3
x −3
Puede observarse que x = 3 es raíz del polinomio del numerador y del
denominador, puede resolverse la indeterminación factorizando y simplificando los
factores en violeta:
( x − 3)( x + 5)
= lim ( x + 5 ) = 8
x →3
x →3
x −3
=
f ′(a ) lim
7
Recta Secante y Tangente – Matemática – Escuela Técnica ORT – 2013 – Ezequiel Wajs
Método 2 (Cociente Incremental)
Para este caso el punto fijo es el mismo. Y la condición que hay que imponer es que
la distancia al siguiente punto (Δx) tienda a cero. De esta forma:
= m=
f ′(3)
tg
∆y
f (3 + ∆x) − f (3)
= lim
∆x ∆x →0
∆x
Para resolver la indeterminación reemplazamos f(x) por su expresión algebráica,
esta vez, especializada en (3+Δx):
(3 + ∆x) 2 + 2(3 + ∆x) + 1 − 16
f ′(3) = lim
∆x → 0
∆x
Aplicando la propiedad distributiva:
9 + 6∆x + ∆x 2 + 6 + 2∆x + 1 − 16
f ′(3) = lim
∆x → 0
∆x
∆x 2 + 8∆x + 16 − 16
∆x 2 + 8∆x
= lim
f ′(3) = lim
∆x → 0
∆x → 0
∆x
∆x
Sacando factor común Δx y simplificando los factores en violeta se resuelve la
indeterminación:
∆x(∆x + 8)
= lim (∆x + 8)
= 8
∆x → 0
∆x → 0
∆x
= lim
f ′(3)
Cómo puede verse ambos métodos arrojan los mismos resultados y son análogos. Y ahora
si, podemos decir, sin miedo a cometer equivocaciones que para el punto X = 3, la función
f(x) crece y que la pendiente de su recta tangente es 8.
8
Recta Secante y Tangente – Matemática – Escuela Técnica ORT – 2013 – Ezequiel Wajs