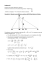DELTA – MASTER

DELTA – MASTER
FORMACIÓN UNIVERSITARIA
C/ Gral. Ampudia, 16
Teléf.: 91 533 38 42 - 91 535 19 32
28003 MADRID
8 – JUNIO – 04
Matemáticas
E1
EXAMEN FINAL MATEMÁTICAS E1 8-JUNIO-2004
PRIMERA PREGUNTA
Sea f: D ⊂ R → R una función diferenciable sucesivamente en el punto x0 ∈ D. Se
pide:
1.- Demostrar que condición debe cumplir dicha función para poder afirmar
que tiene un punto crítico en x0
2.- Demostrar una condición suficiente que permita afirmar que dicha función
tiene un máximo local estricto en x0
1.- Sea f: D⊂ R→ R
D≡ (a,b) con a < b
x0∈(a,b)
Derivable hasta n con derivadas continuas en x0.
Suponemos que :
fk) (x0)=0
∀k∈Ν / 1≤ k ≤ n
n)
f ≠0
Si n es par tendremos un extremo local y si n es impar tendremos un punto de inflexión.
a) Haremos primero la demostración para n par:
(CNS) para que f tenga un mínimo local (máximo local) estricto: f n) (x0)>0. Demostración:
· Necesaria (⇒)
Si f tiene mínimo local estricto ⇒f n)(x0)>0
Hipótesis de partida:
∃ de un mínimo local estricto. Desarrollo de Taylor (Función diferenciable)
f(x) tiene un mínimo local estricto en x0 ...
f ′′(x 0 )
f k) (x 0 )
f n) (z 0 )
f(x)=f(x0)+f’(x0)(x-x0) +
(x − x 0 ) n)
( x − x 0 ) 2 + ... +
(x − x 0 ) k +
2!
k!
n!
con z0∈(x,x0) ó z0∈(x0,x)
f n) ( z 0 )
f(x)-f(x0)=
( x − x0 ) n
n!
Si n es par ⇒ (x-x0)n>0
n!>0
f n)(z0) > 0
b) Si n es impar veamos que es un punto de inflexión.
Por el hecho de ser impar tenemos que el punto no puede ser ni máximo ni mínimo por lo que solo
puede ser un punto de inflexión.
2.- La condición suficiente sería comprobar que si f n)(x0) < 0 con n par ⇒ f(x) tiene un máximo local
estricto en x0.
Usamos de nuevo el desarrollo de Taylor:
f ′′(x 0 )
f k) (x 0 )
f n) (z 0 )
( x − x 0 ) 2 + ... +
(x − x 0 ) k +
f(x)=f(x0)+f’(x0)(x-x0) +
(x − x 0 ) n)
2!
k!
n!
con z0∈(x ,x0) ó z0∈(x0 ,x)
1
8 – JUNIO – 04
Matemáticas
E1
DELTA – MASTER
FORMACIÓN UNIVERSITARIA
C/ Gral. Ampudia, 16
Teléf.: 91 533 38 42 - 91 535 19 32
28003 MADRID
f n) ( z 0 )
f(x)-f(x0)=
( x − x0 ) n
n!
Si n es par ⇒ (x-x0)n>0
n!>0
y f n)(x0) < 0
f n) ( z 0 )
Por tanto f(x)-f(x0)=
( x − x 0 ) n <0
n!
Así que f(x)<f(x0) que es la definición de máximo local estricto.
SEGUNDA PREGUNTA
El número de bacterias por centímetro cúbico que hay en un lago público por días
,después de un determinado tratamiento químico, viene determinado por la
función: B(x) = 13x2 –78x + 650
¿Cuántos días debe durar el tratamiento para que la cantidad de bacterias sea
mínima?
Sea X ≡número de días y B(x)≡ número de bacterias
Para buscar el mínimo a B(x) aplicamos la condición necesaria (B′(x) ) = 0
B′(x ) = 26x-78 = 0 ⇒ x = 78/26 = 3
Para comprobar que es mínimo aplicamos la condición suficiente que es B′′ (x0)>0
B′′ = 26 > 0 por lo que x = 3 es un mínimo.
El tratamiento debe durar 3 días.
TERCERA PREGUNTA
Sea f: D ⊂ R2 → R una función de la forma z = f(x,y) y sea un punto del dominio
x 0 = (x 0 , y 0 ) Se pide:
r
1.- Concepto de derivada direccional en x 0 según la dirección del vector v
2.- Supuesto que dicha función es diferenciable en dicho punto ¿Cuál sería la
expresión de dicha derivada direccional?
3.- ¿Cuándo podríamos afirmar que la derivada direccional coincide con la
derivada parcial respecto de y? Razona la respuesta.
{
}
1. - D v = x ∈ R n /x = x 0 + λv
x → x 0 cuando λv → 0
v es fijo y v = 1
f (x ) − f (x 0 )
f ( x 0 + λv ) − f ( x 0 )
f ( x 0 + λv) − f ( x 0 )
= lim
= lim
=
x→x 0
λ →0
λ →0
x − x0
x 0 + λv − x 0
λv
f ( x 0 + λv) − f ( x 0 )
f ( x 0 + λv ) − f ( x 0 )
f ( x 0 + λv) − f ( x 0 )
= lim
= lim
= lim
λ →0
λ →0
λ →0
v λ
λ
λ
f vr′ (x 0 ) = lim
t
2.- Si z es diferenciable en x 0 entonces f v′ ( x 0 ) = ∇ t f( x 0 )·v siendo ∇ f( x 0 ) = (f x′ ( x 0 ), f y′ ( y 0 )) el
vector gradiente de la función.
3.- La derivada direccional, coincidirá con la derivada parcial respecto de y, en la dirección de vector
(0,1)
2
8 – JUNIO – 04
Matemáticas
E1
DELTA – MASTER
FORMACIÓN UNIVERSITARIA
C/ Gral. Ampudia, 16
Teléf.: 91 533 38 42 - 91 535 19 32
28003 MADRID
CUARTA PREGUNTA
Sea la ecuación F(x,y,z)= 3x2yz-yLx-3=0. Se pide:
1.- Estudiar la existencia de las funciones implícitas x = f1(y,z); y = f2(x,z);
z = f3(x,y) en el entorno del punto x 0 = (1,1,1)
∂z ∂y
y
∂x ∂z
1.- Las condiciones que deben verificarse son: F:D ⊂ R3 → R
a) F(x,y,z) es continua en (x0,y0,z0) y en su entorno.
b) F(x,y,z) = 0 en (x0,y0,z0).
c) Existen las dos derivadas parciales de las variables de las que dependa.
d) La derivada parcial de la función en el punto es distinta de cero.
2.- Calcular, si es posible
a) La función F(x,y,z) es continua por ser composición de funciones continuas en el punto
(1,1,1) y en todo un entorno suyo. El único problema podría estar en el logaritmo pero en este
caso al ser el punto (1,1,1) no hay problema.
b) F(1,1,1)=3·1·1·1-1·L1-3=0
y
∂F
∂F
∂F
c)
= 6xyz −
= 3x 2 z − Lx
= 3x 2 y
x
∂x
∂y
∂z
Las tres derivadas son continuas en el punto (1,1,1)
Para f1 tenemos que las derivadas respecto de y y de z son continuas, para f2 son continuas las
derivadas respecto de x y de z y por último para f 3 son continuas las derivadas respecto de x y
de y.
∂F
∂F
∂F
d) Para f1 ;
≠ 0; Para f2 ;
≠ 0; Para f3 ;
≠ 0 en el punto (1,1,1)
∂x
∂y
∂z
Por tanto existen las tres funciones implícitas.
2.- Calculamos las siguientes derivadas parciales:
y
∂F
∂F
6xyz −
2
∂x
∂y
∂z
∂z = − 3x y
x
=−
=−
=
−
∂F
∂F
∂x
∂z
3x 2 y
3x 2 z − Lx
∂z
∂y
QUINTA PREGUNTA
Sean las funciones f(x,y)= sen
x
y g(x,y)= cos xy. Se pide:
y
1.- Analizar la dependencia funcional de ambas funciones.
2.- Comprobar si algunas de dichas funciones son homogéneas, dando su grado de
homogeneidad.
1.- Para la dependencia funcional utilizamos el Jacobiano.
1
x −x
x
 f x′ f y′   cos
cos 
2
= y
J = 
y
y  calculamos el determinante y da
y

 g ′x g ′y   − ysenxy − xsenxy 
-x
x
x
x
- 2x
x
cos senxy − cos senxy =
cos senxy
y
y
y
y
y
y
3
8 – JUNIO – 04
Matemáticas
E1
DELTA – MASTER
FORMACIÓN UNIVERSITARIA
C/ Gral. Ampudia, 16
Teléf.: 91 533 38 42 - 91 535 19 32
28003 MADRID
Para que sean funcionalmente dependientes el determinante debe ser cero para todo punto del
dominio, cosa que no ocurre. Por lo tanto las funciones son independientes
2.- Para comprobar si es homogénea se tiene que verificar f (tx, ty ) = t α f (x, y )
tx
x
f(tx, ty) = sen = sen = f(x, y), la función es homogénea de grado cero
ty
y
g(tx, ty) = costxty = cost 2 xy ≠ t α g(x, y) la función no es homogénea.
SEXTA PREGUNTA
Resolver las siguientes integrales:
(Lx ) dx
1
2.- ∫
∫ x 2 − 1 dx
x
1. - Es una función racional. con grado mayor en el denominador x 2 − 1 = 0, x = ±1
3
1.-
A
B
1
dx = ∫
dx + ∫
dx
x +1
x −1
−1
A(x − 1) + B(x + 1)
1
A
B
Calculamos A y B : 2
=
+
=
x −1 x +1 x -1
x2 −1
1 = A(x − 1) + B(x + 1)
∫x
2
Para x = 1 ⇒ B = 1
2
Para x = -1 ⇒ A = - 1
2
-1
1
-1
1
1
1
2
2
∫ x 2 − 1 dx = ∫ x + 1 dx + ∫ x − 1 dx = 2 L(x + 1) + 2 L(x − 1) = 2 [L(x − 1) − L(x + 1)] =
1 x -1
 x -1 
L
= L

2 x +1
 x + 1
1
2
x -1
+C
x +1
=L
2. − Es una integral inmediata, del tipo ∫ u n ⋅ u ′dx =
Por lo tanto
∫
(Lx )3 dx = (Lx )4
x
4
u n +1
+ c; donde u = Lx
n +1
+C
SÉPTIMA PREGUNTA
π
3
1
dF(x) si
2
0 cos x
Resolver la siguiente integral ∫
1.- F(x) = 2x
π

1 0 ≤ x < 4
2.- F(x) =  π
π
≤x≤
5
4
3

1.- Es una integral de Stieltjes del tipo
π
3
π
[
3
1
2
d2x
dx = 2tg x
=
∫
∫ g(x)dF(x) = ∫ g(x)F′(x)dx ∫
2
2
0 cos x
a
a
0 cos x
b
b
]
π
0
3
(
)
= 2 tg π - tg0 = 2 ⋅ 3
3
4
8 – JUNIO – 04
Matemáticas
E1
DELTA – MASTER
FORMACIÓN UNIVERSITARIA
C/ Gral. Ampudia, 16
Teléf.: 91 533 38 42 - 91 535 19 32
28003 MADRID
b
2.- Esta integral es de Stieltjes del tipo ∫ g(x)dF(x) = ∑ s i ⋅ g (c i ) Representamos la función.
a
i
5
1
0
π/4
π/3
Se produce un salto en el punto c1 = π/4 y de valor s1= 4. Como
1
1
4
1
1
; g (c1 ) =
=
g ( x) =
=
= =2
2
2
2 π
2
2
cos x
cos
4
4  2 
 2
( )
b
Esto quiere decir que la integral ∫ g(x)dF(x) = 4 ⋅ 2 = 8
a
OCTAVA PREGUNTA
Concepto de función integral. Demostrar que la función integral es una función
continua.
Sea la f (x) integrable en el sentido Riemann en [a, b], por la aditividad respecto del intervalo de
u
integración ∃∫ f(x)dx , , [a, u ] ⊂ [a, b]
a
F : [a, b] → R
u
,
F(u ) = ∫ f (x )dx es la función integral
a
NOVENA PREGUNTA
Definir y explicar los conceptos de:
1.- Ley financiera.
2.- Tanto de interés efectivo fraccionado a corto plazo.
3.- Tipos de leyes de descuento.
1.-Es la función matemática a través de la cual, dado un capital financiero (C,t) y fijado un punto de
aplicación P; permite obtener su capital financiero equivalente (V,p).
Es una función que permite determinar la variación del capital en el tiempo. Existen 2 tipos de leyes
financieras: Ley de capitalización y ley de descuento.
2.- i = im·m. Es la variación experimentada por la cuantía por unidad de capital y por el
fraccionamiento del tiempo.
3. Hay tres :
5
DELTA – MASTER
FORMACIÓN UNIVERSITARIA
C/ Gral. Ampudia, 16
Teléf.: 91 533 38 42 - 91 535 19 32
28003 MADRID
8 – JUNIO – 04
Matemáticas
E1
a) Ley de descuento comercial. Se produce descuento cuando los acreedores acuden a
intermediarios financieros para percibir los cobros pendientes con antelación al vencimiento de
estos. Se usa a corto plazo. Es una función decreciente.
b) Ley de descuento racional. Es la inversa de la ley de capitalización simple. Suele usarse a corto
plazo. Proporciona mejores valores que el comercial.
c) Ley de descuento compuesto. Es la operación financiera consistente en la sustitución de un
capital futuro a más de un año por otro con vencimiento presente. Es la operación inversa a la
de la capitalización compuesta.
DÉCIMA PREGUNTA
Una persona de 47 años recibe una herencia de 100.000 euros que decide colocar
en un depósito para rescatar a la hora de la jubilación e irse a dar la vuelta al
mundo. Encuentra un banco que le ofrece un depósito que le reportará un tanto
de un 6% durante los diez primeros años y un 7% mensual a partir de esa fecha
que se actualizará en un 1% más cada 5 años.
En el momento de su jubilación , ¿con qué capital cuenta para poder hacer su
viaje?
Dividimos el problema en tres partes:
Desde los 47 a 57 años. Los 10 primeros años a un 6%.
Desde los 57 a 62 años. Cinco años al 7% mensual.
Desde los 62 a los 65 años. Edad de jubilación.
Utilizamos la ley de capitalización compuesta por ser el periodo superior a 1 año:
-primer tramo.
C = 100.000

z
10
i = 6% C z = C(1 + i ) = 100.000(1 + 0.06) = 179084'769
z = 10 
-segundo tramo.
C = 179084'769

z
60
i = 7% mensual C z = C(1 + i ) = 179084'769(1 + 0.07 ) = 10377322'46

z = 60

-tercer tramo.
C = 10377322'46

z
36
i = 8% mensual C z = C(1 + i ) = 10377322'46(1 + 0.08) = 165706868'25

z = 36

Esta es la cantidad con la que se jubilará.
6